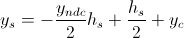Picking

마우스 혹은 기타 입력 장치로 모니터 화면의 좌표를 지정하면 3D 세계에 있는 오브젝트를 선택할때 사용된다.

화면의 좌표는 2D, 세계는 3D인 경우 오브젝트의 선택 방법을 만들어야 한다.

먼저 화면에서 지정한 좌표를 이용하여 3D 세계로 광선을 발사하여 교차되는 오브젝트를 찾으면 된다.

간단한 그래픽 파이프라인을 생각해 보자

월드 변환-> 뷰 변환-> 투영 변환-> 화면 변환

이 과정을 거꾸로 거쳐서 화면에서의 점을 월드 좌표계로 만든다.

첫번째로 화면변환(ScreenTransform)-> 투영변환(ProjectionTransform)을 고려해 보자

뷰 공간에서 투영 변환이 끝난 공간은 NDC(Normalized Device Coordinates)가 된다.

잠시 원래 과정인 NDC-> Screen Coordinates을 생각해 보면 아래와 같은 공식이 나오게 된다.





참고: 화면변환

: 화면 좌표계의 좌측 상단 x 좌표

: 화면 좌표계의 좌측 상단 y 좌표

: 화면 좌표계의 화면 Width

: 화면 좌표계의 화면 Height

: 화면 좌표계의  x 좌표

: 화면 좌표계의  y 좌표

위 식에서 필요한것은 NDC의 값이므로 위 식을 ndc에 대해 정리 한다.

두번째로 필요한 것은 NDC에서 ->View frame으로 변환이 필요하다.

먼저 z값을 생각해 보자.

현재 화면 변환-> 투영 변환을 거쳐서 좌표값은 NDC에 있으므로 

z값은 투영 평면(projection plane)위에 놓여진 상태이며

따라서 z값은 투영 평면 거리 값 d를 그대로 사용하면 된다.

,

그리고 좌표 값이 투영 평면에 위에 있으므로  x, y 값은 투영변환이 끝난 상태 이다.

NDC 에서 x의 범위는 [-a, a] 이고 y의 범위는 [-1, 1]이 된다.

여기서 a는 aspect값을 나타낸다.

aspect=(screen_width / screen_height)

이제 투영변환 되기 전의 x, y 값을 구해야 한다.

원래 변환 과정를 생각해 보면 

View Frame에서 NDC로 변환 될때 위에서 나타낸 x, y의 범위로  Scale이 되었다.

그러므로 변환되기전 좌표값을 찾아낼려면 반대로  x, y의 값을 Scale 하면 된다.

먼저 y의 범위는 [-1, 1]이므로  Scale이 필요 없이 그대로 사용하면 되고

x의 범위는 [-a, a]이므로 a의 값 만큼 Scale이 필요하다.

ndc에서의 x, y값을 위의 설명에 따라  Scale을 해주면 다음과 같이 된다.

 

그리고 z값은

(DirectX 의 경우 Z 방향은 화면 안쪽 방향이 되어  +d값이 사용 된다.)

세번째로 월드 좌표에 있는 모델과 충돌 시킬 광선(Ray)을 만든다.

현재까지 구해진 좌표값을 이용하여 광선을 만든다.

먼저, 좌표값은 View Frame에 있으므로 World 좌표계로 변환이 필요하다.

방법은 뷰 변환에 사용하는 뷰 변환 행렬의 역행렬을 곱하면 World 좌표값을 구할 수 있다.

그리고 카메라의 위치값(Eye Position)을 사용한다.

따라서 충돌에 사용할 광선은 다음과 같이 된다.

마지막으로 World 좌표계에서 위의 광선과 충돌 여부를 판단한다.

카메라 위치에서 광선을 만들어 충돌을 판단하게 되므로 여러 개의 모델이 광선과 충돌할 수 있다.

충돌하는 모델 중 광선의 t 값이 가장 작을 경우가 처음으로 광선과 모델이 충돌되는 경우가 되며

이것이 picking 되는 모델이 된다.

상황에 따라 광선을 각 모델 좌표계로 변환하여 해당 모델 좌표계에서 계산할 수도 있다.

참고자료

Essential Mathematics for Games & Interactive Applications Second Edition

자주 사용하는 emacs 명령어 정리(1)

문서 편집에 필요한 기본 명령어들을 정리

notepad++ 이나 free commander를 사용하지 않을 만큼 추가 정리 필요

 c: ctrl key
m: alt key or esc key

------------------------------------------------------------------------------
move
c-f: right
c-b: left
c-n: down
c-p: up
c-a: first of the current line
c-e: last of the current line
m-f: forward by word
m-e: back by word
c-v: forward page
m-v: back page
m-<: buffer="" first="" of="" p="">m->: last of buffer

save: c-x c-s
save as: c-x c-w

replace text: m-% (condition: y, n, !(total))

regexp search: esc c-s (forward)
regexp search: esc c-r (back)

------------------------------------------------------------------------------
window

c-x 1: remain only current window
c-x 2: split window horizontal
c-x 3: split window vertical

------------------------------------------------------------------------------
edit

c-x tab: indent current region
c-o: insert blank line after the cursor
c-shift-@: set mark
m-w: copy
c-y: paste
c-w: cut
c-shift-_: undo
c-u nubmer: repeat number time

c-g: cancel current command
c-x k: kill current buffer

------------------------------------------------------------------------------
select rectangle region

1. m-x cua-mode
2. c-return
3. move (using arrow keys or emacs move keys )
4. copy, cut, paste( c-x, c-c, c-v or emacs command keys)

------------------------------------------------------------------------------
mode

m-x column-number-mode: show column number
m-x cua-mode

------------------------------------------------------------------------------
dired mode

c-x c-f: open file
c-x d: open directory
p: up
n: down
C: copy
D: delete
m: set mark
u: disable mark
U: disable all mark

Screen Transform (화면 변환)

Screen Transform

투영 변환이 끝난 후의 좌료계는 NDC(Normalized Device Coordinates)로 바뀌게 된다.

이 좌표계는 중심이 (0,0)이고 가장자리 까지 거리가 1인 공간이다.

우리가 보는 화면으로 나타내기 위해서는 이 좌표계에 있는 점들을 화면 좌표계(Screen Coordinates)로 변환하여야 한다.

이때 Viewport정보가 사용 된다.

화면 좌표계는 좌측 상단을 (0,0)으로 가지고 우측 하단을 (Width_screen, Height_screen)으로 가지게 된다.

NDC에서 화면 죄표계로 변환을 y 값 부터 생각해 본다.

NDC에서 y의 범위는 [-1, 1]이므로 화면 좌표계의[0, Height_screen]으로 바꾸어야 한다.

1. y범위가 2배 단위 이므로 절반으로 나누어 1배 단위로 만들고 Height_screen값을 곱하여 늘려준다.

2. NDC의 y 방향과 화면 좌표계의 방향은 반대 이므로 Flip 하여 준다.

3. 화면 좌표계는 좌측 상단(0,0)부터 시작 하므로 Height_screen의 높이의 절반을 더하여 상단으로 이동시켜 준다.

4. x값의 경우, NDC에서의 x 좌표 방향과 화면 좌표계의 x 방향이 같으므로 Flip 과정이 필요 없다.

    그러므로 2번 과정을 제외한 1, 3번 과정을 동일하게 적용하여 값을 구한다.

지금까지 구해진  x_s, y_s 는 화면 좌표계에서 화면의 좌측 상단이 (0, 0)일때를 고려 하였다.

하지만 경우에 따라 좌측 상단이 이 다른 값을 가질 수도 있다.

특정 좌측 상단값을 (x_c, y_c)이라고 할 경우

지금 까지 구해진  x_s, y_s값에 추가로 더하여 주기만 하면 된다. 

마지막으로 z값은 깊이 테스트에 사용하기 위해서

NDC의 범위 [-1, 1]에서  [0, depth_screen]으로 변환해 주어야 한다.

depth_screen값은 보통 1을 사용한다.

x_s 값을 구하는 과정과 똑같이 1, 3번 과정을 거치면 최종 z_s 값은 다음과 같아 진다. 

NDC에서 화면 좌표계로의 변환을 행렬로 나타낼 수 있다.

DirectX 경우  NDC의 z 범위는 [0, 1]을 사용하고 있다. 

따라서 z값을 절반으로 나눌 필요 없이 바로 depth_screen 값을 곱하여 늘려 주며

3번 과정 처럼 추가적으로 z값을 이동 시켜 줄 필요도 없다.

결과적으로 z값은 다음과 같다.

그래서 DirectX에서 사용되는 행렬은 아래와 같이 된다.

참고자료

Essential Mathematics for Games & Interactive Applications Second Edition

Perspective Projection (원근 투영)

설명의 시작은 오른손 좌표계(OpenGL)를 기준으로 시작한다.

투영(Projection)을 하기전에 모든 좌표값은 카메라 공간으로 이동된 상태가 되며

이번에는 원근 투영을 정리할 것이므로 절두체를 이동하여 투영을 계산하게 된다.

이때 투명을 하게 되면 절두체를 정방형공간으로 바꾸는 과정이 이루어 진다.

첫번째로 일단 z의 범위는 생각 하지 않고 x,y를 먼저 투영평면에 투영을 한다.

변환하게 될 정방형 공간의 범위에 따라서 투명평면의 x,y 범위는 [-1, -1] ~ [1, 1]이 된다.

먼저 y를 투명해 보기로 한다.

절두체를 yz폄명으로 잘라서 보자.

절두체에서 y_max의 값을 투영 폄면에 투명하게 되면 

투영평면의 y범위에 따라서 y_p는 1값을 가지게 된다.

그리고 닮은꼴 삼각형에 따라서 

y / -z = y_p / d가 성립하게 되고  y_p = dy /-z가 되어 y_p를 구할 수 있게 된다.

하지만 여기서 원점에서 투명 평면까지 거리인  d를 구해야 한다.

d는 간단한 삼각형 공식을 이용해 구해진다.

tan (Ɵ / 2) =  1 / d

d = 1 / tan (Ɵ / 2), d = cot (Ɵ / 2)

두번째로 x값도 y값을 구하는 과정과 동일하게 구할 수 있지만

투명평면은 정사각형이 아닌 직사각형 형태이다. 

일단 첫번째와 동일 과정을 거치면

x / -z = a x_p / d가 되고 여기서 a값은 직사각형 형태를 만들어 주기 위한 종횡비값을 나타낸다.

a = width / height이고 정리를 하면 

x_p = dx / -za 가 된다.

이제 변환된 새로운 좌표를 동차표현식으로 나타내면 다음과 같아 진다.

x_new = dx / a

y_new = dy

z_new = dz

w = -z

그리고 w로 각 요소를 나누면 투영 변환 후의 좌표를 확인할 수 있다.

x_w = dx / -za

y_w = dy / -z

z_w = -d

w_w = 1

이제 w로 나누기전의 식들을 행렬로 나타내면 아래와 같다.

| d/a 0    0   0 |

| 0     d    0   0 |

| 0     0    d   0 |

| 0     0   -1   0 |

이 행렬에 변환되지 않은 x, y,z를  곱하면  변환된  x, y, z를 확인할 수 있다.

| d/a 0    0   0 |    |   x  |   =    |   dx / a |  

| 0     d    0   0 |    |   y  |   =    |   dy       |  

| 0     0    d   0 |    |   z  |   =    |   dz       |  

| 0     0   -1   0 |    |   1  |   =    |   -z       |

현재까지 z값을 고려하지 않고 행렬을 만들었다.

이제 z값을 [near, far] 범위로 변환해야 한다.

near = 원점 부터 near 평면까지의 거리

far = 원점부터  far 평면까지의 거리

z범위 변환을 위해 위에서 구해진 행렬에 추가 과정를 더 거친다.

1. [ -n, -f]의 범위를 정방형 범위인 [ -1, 1 ]로 Scaling

2. [ -1, 1 ]로 이동

(오른쪽  좌표계 기준이므로 z 방향은 화면 바깥 방향을 가리키고  n, f는

 크기만을 나타내므로 - 부호가 붙어 지게 된다.)

참고로 4x4 Affine 행렬에서 

Scale 인자는 행렬의 대각선분에 

Translation 인자는 마지막 열에 나타내게 된다.

| S_x    0       0         T_x |

| 0        S_y   0         T_y |

| 0        0        S_z    T_z |

| 0        0       0         1      |

이전에 구한 행렬에서 z값에 2가지 과정를 반영하면

| d/a 0    0   0 |      =>      | d/a 0    0   0 |

| 0     d    0   0 |                 | 0     d    0   0 |

| 0     0    d   0 |                 | 0     0    A  B |

| 0     0   -1   0 |                 | 0     0   -1  0 |

이제부터는 변환 과정이 반영된 A, B를 구해본다.

먼저 near 폄면에 대해서 계산해 보자.

| d/a 0    0    0 |    |   0  |   =    |   0             |  

| 0     d    0    0 |    |   0  |   =    |   0             |  

| 0     0    A   B |    |  -n  |   =    |   -nA + B  |  

| 0     0   -1   0 |    |   1  |   =     |   n             |

w값으로 나누어 보면

z_w =  -A + B / n

z_w는 near 평면의 거리이므로 -1이 되고 대입해 보면

-1 = -A + B / n,     B = (A-1) / n

잠시 여기서 멈추고  far 평면에 대해서 계산해 보자.

| d/a 0    0    0 |    |   0  |   =    |   0             |  

| 0     d    0    0 |    |   0  |   =    |   0             |  

| 0     0    A   B |    |  -f   |   =    |   -fA + B  |  

| 0     0   -1   0 |    |   1  |   =     |   f             |

w값으로 나누면 

z_w = -A + B / f

z_w는 far 평면의 거리이므로 1이 되고 대입을 해 보면

1 =  -A + B / f

이 시점에서 위에서 구한  B값을 대입하여  A값을 구한다.

1 =  -A + ( (A-1) / n ) / f 

A에 대하여 정리를 하면

A = n + f / n - f

구해진  A를 처음에 구해진 B식에 대입하여 B를 구한다.

B = (A-1) / n

B = ( ( n + f / n - f ) - 1 ) / n

B에 대하여 정리를 하면

B = 2nf / n - f

최종적으로 구해진 A, B값을 대입하여 원근 투영 행렬은 다음과 같아진다. 

(OpenGL 경우)

| d/a     0    0                  0             |

| 0         d    0                  0             |

| 0         0    n+f / n-f     2nf / n-f |

| 0         0   -1                  0             |

DirectX의 경우

z의 범위는 [0, 1]이 되고

z의 방향도 반대가 된다. (화면 안쪽을 가리킴)

z값을 고려하기 전 행렬은 다음과 같아지고 

| d/a 0    0    0 |

| 0     d    0    0 |

| 0     0    A   B |

| 0     0   1     0 |

z값의 범위를 다시 고려하여 A, B를 구하면

A = f / f - n

B = -nf / f - n

행렬은 다음과 같아진다.

| d/a     0    0                  0             |

| 0         d    0                  0             |

| 0         0    f / f - n     -nf / f - n   |

| 0         0   1                  0              |

마지막으로 DirectX은 행벡터 기준이므로 전치행렬을 만들어 사용한다.

| d/a     0    0                  0     |

| 0         d    0                  0     |

| 0         0    f / f - n        1     |

| 0         0   -nf / f - n     0     |

참고자료

Essential Mathematics for Games & Interactive Applications Second Edtion

광선과 평면 교차 ( Intersecting segment(ray) and plane )

선분 ab는 다음의 식으로 표현할 수 있다.

s(t) = a+ t (b - a) 

a는 선분의 시작점(org)을 나타내다.

(b - a)는 선분의 방향(dir)을 나타내고 크기는 1이 된다.

그리고 t는 선분 상의 위치를 나타내는 변수이고, 0 이상 1이하의 값을 가지게 된다.

여기서 

t 값이 +. -  방향 모두 무한대가 되면 직선, 

t 값이 한쪽 방향으로만 무한대가 되면 반직선이 된다. 

평면과 교차할때 직선의 t 값을  알아내면  교차점을 알아낼 수 있다.

평면의 식을 다음과 같이 나타내고 

n ∙ x + d = 0

특정 t 값 일때의 선분을 위 식에 대입한다.

n ∙ ( a+ t (b - a))  + d = 0

식을 t 에 대하여 정리하게 되면 아래과 같이 된다.

t = ( -n∙ a - d ) / ( n∙(b - a))

계산한 결과 t 값이 0 이상 1 이하라면 해당 평면과 선분을 교차하게 된다.

반직선의 경우는 검사하는 t 값을 범위를 조절하면 

평면과 반직선의 교차 여부를 판단할 수 있다.

-->

 1 bool segment_plane(vector3& org, vector3& dir, plane& p,
 2                 vector3& out_res)
 3 {
 4         float t = (-vec3_dot(p.normal, org) - p.d) /
 5                         vec3_dot(p.normal, dir);
 6 
 7         if(t >= 0.0f && t <= 1.0f)
 8         {
 9                 out_res = org + t * dir;
10                 return true;
11         }
12         return false;
13 }

참고문헌:
Real-Time Rendering 2판
Real-Time Collision Detection

AABB와 구 교차 ( Intersecting AABB and sphere )

AABB의 점들 중에서 구의 중심과 거리가 가장 가까운 점을
찾아서 충돌 확인한다.

AABB이므로 각 축별로 구의 중심과 거리를 확인한다.

구의 중심이 v_min과 v_max 사이에 있을 경우는 서로 교차하므로
따로 검사가 필요 없다.

-->

bool CollisionSphereAABB(Sphere& s, AABB& aabb) {
        float dist = 0.0f;

        for(int i=0; i<3; i++)
        {
                if( s.center[i] < aabb.v_min[i] )
                {
                        d += ((aabb.v_min[i] - s.center[i]) *
                                (aabb.v_min[i] - s.center[i]));
                }
                else if( s.center[i] > aabb.v_max[i] )
                {
                        d += ((s.center - aabb.v_max[i]) *
                                (s.center - aabb.v_max[i]));
                }
        }

        if( dist > s.center * s.center )
                return false;

        return true;
}

참고 문헌
Real-Time Rendering 2판
Real-Time Collision Detection

AABB와 평면 교차 ( Intersecting AABB and plane )

AABB에는 4개의 대각선이 존재
중점 C을 지니고 각 꼭지점을 이어서 나온 대각선들

먼저 충돌 검출할 평면의 n과 가장 평행한 대각선을 찾음
그러면 대각선의 양 끝점 vmin, vmax를 찾게 됨

이 v를 평면 방정식에 대입하여 위치를 판단한다.

n • v + d = 0

1. 두 점의 결과가 양의 영역에 있다면 평면의 바깥쪽에 AABB가 있음

2. 두 점의 결과가 음의 영역에 있다면 평면의 안쪽에 AABB가 있음

3. 두 점의 결과가 다른 경우 평면과 교차함

int CollisionAABBPlane(const D3DXVECTOR3* pMin, const D3DXVECTOR3* pMax, const D3DXPLANE& p)
{
 D3DXVECTOR3 NewMin, NewMax;

 for( int i=0; i<3; ++i)
 {
  if( p[i] >= 0)
  {
   NewMin[i] = pMin[i];
   NewMax[i] = pMax[i];
  }
  else
  {
   NewMin[i] = pMax[i];
   NewMax[i] = pMin[i];
  }
 }

 if( D3DXPlaneDotCoord(&p, &NewMin) > 0 )
 {
  return FRONT; 
 }

 if( D3DXPlaneDotCoord(&p, &NewMax) < 0 )
 {
  return BACK; 
 }

 return INTERSECT;
}

참고 자료: Real- Time Rendering 2판