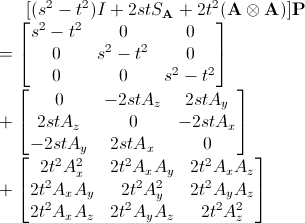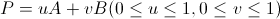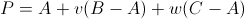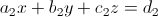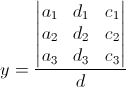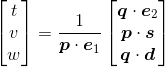사원수 회전 (Quaternions Rotation)

사원수(Quaternions)의 회전은 아래와 같이 나타낼 수 있다.
P: 회전이 필요한 점
q: 회전축 및 각도가 표현된 사원수




s: scalar value
v: vector value

그럼 위 식을 차례대로 풀어서 정리해 보자.

먼저 아래 공식을 기억해 두고 하나씩 정리한다.

스칼라 및 벡터 연산에 대하여 주의하면서 풀어나가면 된다.
위 식에서 앞 부분을 조금 풀어보면

그리고 게속해서 나머지를 정리한다.

여기서 v를 단위벡터A와 길이 t로 표현하여 위의 식을 계속 정리하면

S_A:skew matrix of A
I: identity matrix

그리고 Axis-Angle Rotation으로 표현했던 아래 식을 상기 시켜
위의 식과 비교해 보면 다음과 같은 결과가 나온다.

위의 3개 식을 풀어서 s, t값을 구한다.
풀이에는 삼각함수의 반각공식(half-angle relations)을 사용하면 된다.

구해진 s, t를 사용하여 사원수 q를 다시 표현하면 다음과 같아진다.

: unit vector of A


이것으로 쿼터니언에서 표현되는 회전각은 1/2값임을 알 수가 있다.

위에서 구해진 식에서 앞쪽 행렬 부분이 사원수의 회전 표현식이 되고
이것을 계속 행렬로 정리한다.

여기서 정리 하기 전에 아래의 관계를 적용한다.

계속해서 행렬을  정리해 나가면

식을 좀 더 간단히 만들기 위해 단위 사원수로 바꾸어 생각한다.
여기서 사원수 q가 단위 사원수가 되면 다음이 성립한다.

이것을 이용해서 행렬식을 다시 정리하면

마지막으로 행렬식을 하나로 합치면

이 행렬식을 사용하여 사원수q를 행렬로 변환하여 사용하면 된다.

참고자료
Essential Mathematics For Games And Interactive Applications
3D 게임 프로그래밍 & 컴퓨터 그래픽을 위한 수학 제2판
Real-Time Rendering 2판

임의의 축 회전 (Axis Angle Rotation)

R² 공간에서 벡터 i=(1, 0)를 회전시 다음과 같이 나타낼 수 있다.

여기서는 기저 벡터를 i, j 대신에 v_perp, w를 사용하고 회전축 A를 이용한다.

v_prop: A축에 대해 projection
v_perp: A축에 대해 perpendicular

위 식은 v의 수직 성분만 있으므로 수평 성분을 더하면 회전된 v를 계산할 수 있다.

그런데 v_prop는 회전축A에 대하여 회전을 하여도 변하지 않게 된다.

그래서 회전된 v는 다음과 같다.

먼저 v_prop를 찾아보자.

회전축인 A에 v를 투영하면 확인할 수 있다.

: A의 unit vector


그리고 v에서 수평 성분인 v_prop를 빼면 수직 성분인 v_perp를 구할 수 있게 된다.

w는 회전축A와 v의 외적으로 구해진다.

위의 회전식을 지금까지 구해진 식으로 풀어서 적으면

그리고 v를 분리하기 위해 tensor product와 skew matrix를 사용하여 정리 한다.

[tensor product]
두개의 벡터 v, w가 있을때

그리고 3개의 벡터 u, v, w가 있을 때

[skew matrix]
외적을 행렬로 표현할때 사용
벡터 v를 skew matrix로 표현하면

그리고 여기에 벡터 w를 곱해주면 외적이 행렬로 표현 된다.

식을 다시 정리하면

S: skew matrix

I: identity matrix

이제 위의 식에서 벡터 v에 곱해지는 부분이 바로 벡터 v를 회전 시키는 행렬 부분이 된다.
다시  행렬 부분만  풀어 적게 되면  다음과 같이 된다.

위의 행렬을 임의의 벡터 v에 곱하게 되면 임의의 회전축 A를 기준으로
회전된 벡터 v를 구할 수 있다.

참고자료
Essential Mathematics For Games And Interactive Applications
3D 게임 프로그래밍 & 컴퓨터 그래픽을 위한 수학 제2판

광선과 삼각형 교차 ( Intersecting ray and triangle )

먼저 무게 중심 좌표(barycentric coordinate)부터 생각해 보자.

무게 중심 좌표는 참조되는 점들의 무게를 조합하는 형식으로 공간을 표현한다.

예를 들어 선분 AB를 생각해 보자

임의의 점 P는  선분  AB 사이에 있는 하나의 점이라고 가정 한다.

그럼 점 P는 아래과 같은 식으로 표현할 수 있다.

P=A + t(B-A)

풀어서 정리하면 다음과 같이 되고

P = A + tB - tA

P = (1-t)A + tB

여기서 표현을 바꾸면

위 식에서 u, v를 무게 중심 좌표(barycentric coordinate)라고 말한다.

참고로 barycentric 이라는 단어에서 bary는 그리스 단어에서 '무게'라는 뜻을 가지고 있다.

삼각형의 경우로 다시 생각하면 삼각형 안의 임의의 점 P 와

동일 선상에 있지 않는 점 A, B, C에 대해서 아래와 같이 나타낼 수 있다.

세번째에 있는 식을 보면 v, w 2개의 변수만 있어도 u를 구할 수가 있다.

그러므로 위 식을 다음과 같이 정리하여 아래에서 계속 사용 한다.

무게 중심 좌표에 따라서 각 u, v, w의 값을 표시 하면 아래과 같은 형태를 생각 할 수 있다.

각 점에서의 u, v, w 값은 아래과 같이 된다.

(u, v, w)

A=(1, 0, 0)

B=(0, 1, 0)

C=(0, 0, 1)

그리고 u, v, w의 값을 확인 하여 임의의 점이 삼각형 안에 있는지 확인할 수 있다.

그럼 이제 삼각형과 교차하는 광선을 생각해 보자.

광선은 아래와 같이 나타낼 수 있다.

o는 광선의 시작점을 나타내고 t는 광선의 길이는 나타내는 스칼라 변수 이다.

그리고  d는 광선의 방향을 나타내는 단위 벡터가 된다.

광선과 삼각형의 교차점은 위에서 설명한 2개의 식을 생각해 본다.

삼각형 안의 임의의 점

광선의 임의의 점

결국 교차점은 삼각형 안의 임의의 점과 광선의 임의의 점이 같을 경우가 된다.

이제 여기서 필요한 t, v, w의 값을 위 식을 계산하여 구해 보자.

 

위 식을 행렬식으로 다시 표현 하면 아래와 같이 된다.

앞쪽에 있는 행렬의 역행렬을 양변에 곱하면 t, v, w의 값을 구할 수 있다.

여기서 역행렬을 구할때는 cramer's rule을 사용 한다.

예를 들어 아래와 같이 3개의 선형 방정식이 있고 원하는 x, y, z 값을 구해야 한다.

 
 

이때 caramer's rule을 적용하면 

,,

식을 간단히 만들기 위해 먼저 d의 determinant식 풀어 본다.

determinant에서는 매트릭스를 전치하여 풀어도 같은 값이 된다. 

위의 d를 아래와 같이 전치하고

d의 determinant 표현을 식으로 풀게 되면 다음과 같다.

위의 식을 정리하면 내적으로 표현할 수 있다.

여기서 각각의 변수를 아래와 같이 벡터로 생각하고

 
 

위 식을 벡터로 표현하면

이제 복잡하게 정리 되었던 x, y, z를 위의 정리를 통해 정리하고

마지막으로 행렬로 다시 표현하면 아래과 같이 표현할 수 있다.

이제 원래대로 돌아가서 t, v, w를 구할 식을 다시 살펴 보자.

식을 간단히 하기 위해 각각의 요소를 아래와 같이 다시 정의 한다.

위 값을 caramer's rule를 사용하여 정리한 식에 대입을 해보자.

여기서 d값이 0이 되면 역행렬은 존재하지 않게 된다. 

그리고 계산량을 줄이기 위해 d값을 먼저 계산하여 변수에 저장하고 다시 사용하도록 한다. 

먼저 - 부호를 제거 하자.

외적의 정의에 따라서 

스칼라 값 r, s이 주어진 경우와 -부호를 적용될 경우 다음과 같다.

또한, Scalar Triple Product 정의에 따라 다음과 같이 된다. 

위의 정의들을 이용하여 식을 정리하면 

계산량 감소 및 재사용을 하기 위해 다음과 같이 정의 한다.

필요에 따라서 t, v, w값을 전부 계산하거나 혹은 부분계산하여 사용하도록 소스를 구현하면 된다.

마지막으로 앞에서 설명하였듯이 t값은 광선을 나타내는 식에 대입하여 사용하고

v, w 값은 삼각형 안의 임의의 점을 나타내는 식에 대입하여 사용하면 된다. 

참고자료

Real-Time Rendering 2판

Real-Time Collision Detection