AABB와 평면 교차 ( Intersecting AABB and plane )

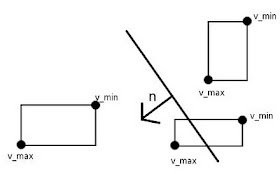
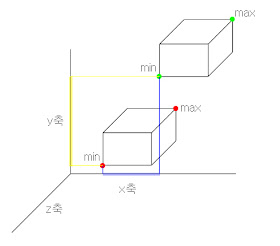
AABB에는 4개의 대각선이 존재
중점 C을 지니고 각 꼭지점을 이어서 나온 대각선들

먼저 충돌 검출할 평면의 n과 가장 평행한 대각선을 찾음
그러면 대각선의 양 끝점 vmin, vmax를 찾게 됨

이 v를 평면 방정식에 대입하여 위치를 판단한다.

n • v + d = 0

1. 두 점의 결과가 양의 영역에 있다면 평면의 바깥쪽에 AABB가 있음

2. 두 점의 결과가 음의 영역에 있다면 평면의 안쪽에 AABB가 있음

3. 두 점의 결과가 다른 경우 평면과 교차함

int CollisionAABBPlane(const D3DXVECTOR3* pMin, const D3DXVECTOR3* pMax, const D3DXPLANE& p)
{
 D3DXVECTOR3 NewMin, NewMax;

 for( int i=0; i<3; ++i)
 {
  if( p[i] >= 0)
  {
   NewMin[i] = pMin[i];
   NewMax[i] = pMax[i];
  }
  else
  {
   NewMin[i] = pMax[i];
   NewMax[i] = pMin[i];
  }
 }

 if( D3DXPlaneDotCoord(&p, &NewMin) > 0 )
 {
  return FRONT; 
 }

 if( D3DXPlaneDotCoord(&p, &NewMax) < 0 )
 {
  return BACK; 
 }

 return INTERSECT;
}

참고 자료: Real- Time Rendering 2판

AABB와 RAY 교차 ( Intersecting AABB and ray )

Slab:

Kay 와  Kajiya가 제안

두 개의 평행한 평면 사이의 무한한 공간

Slab과  Ray의 교차를 이용하여 AABB 교차를 판단

광선(Ray): r(t) = o + td

o: 원점

t: 광선상의 정점들을 생성하는데 사용되는 변수

d: 방향 벡터 ( 일반적으로 편의 위해 정규화 함, ||d|| = 1 )

광선이 Slab의 한 평면과 교차하는 t 값을 구하여 사용

평면:  n + D = 0

평면 위의 한 점 x의 경우 다음을 만족함

n • x + D = 0

그러므로 t 값을 구하기 위해 x를 t값을 가지는 광선의 한점으로 대치함

n • (r(t)) + D = 0

n • ( o + td ) + D = 0

(n • o) + t(n • d) + D = 0

t = ( -(n • o)  - D ) /  (n • d)

여기서  AABB의 특징들을 이용하면 t에 대한 식이 간단히 됨

1. AABB는 표준 기저와 축이 같아서

평면 n의 값이 각 축마다 2개 요소씩 0이 됨

예) x축의 경우: n_x  = (1, 0, 0)

그래서 n_x • o = (1, 0, 0) • (o_x, o_y, o_z) = o_x

 i  ∈ { x, y, z } 이면 위의 t 에 관한 식은 정리 되어서

t = ( -o_i  - D ) /  d_i

2. 추가로 평면이 표준 기저 축과 평행하므로 평면의 D의 값은

AABB의 min[i], max[i]값을 사용할 수 있음 ( i  ∈ { x, y, z } ) 

또한, d_i의 절대값이 아주 작을 경우 해당되는 축과 평행하게 됨

이때는 해당되는 축의 원점 o_i 값이 AABB의 min, max를 

벗어나면 교차 상태가 아니게 됨

광선과 Slab의 평면들과의 교차점을 찾아 t_min, t_max값을 찾는다.

예를 들어 현재 축에 해당되는 Slab 평면과 교차점 찾는 경우

t_min: 광선의 시작점으로 부터 처음 만나는 Slab 평면의 교차점

t_max: 두번째 Slab 평면과 교차점 

이렇게 각 축마다  t값을 구하면서 t_min, t_max가 서로 가까운 거리가 

유지 되도록 한다.

작업 중간에 t_min > t_max 이렇게 값이 서로 바뀌는 경우가 발생하면

AABB는 서로 교차하지 않는 것이 된다.

  

 //o: 광선의 원점

//d: 광선의 방향벡터

//p: 첫번째 교차점

bool AABBtoRay(AABB a, Vector3 o, Vector3 d, Vector3& p)

{

        float t_min = 0;

        float t_max = MAX_FLOAT;

for(int i=0; i<3; i++)

{

if(abs(d[i]) < EPSILON)

{

if( o[i] < a.min[i] ||

  o[i] > a.max[i] )

return false;

}

else 

{

float denom = 1.0f / d[i];

float t1 = (-o[i] - a.min[i]) * denom;

float t2 = (-o[i] - a.max[i]) * denom;

if(t1 > t2)

{

swap(t1, t2);

}

t_min = max(t_min, t1);

t_max = min(t_max, t2);

if(t_min > t_max)

return false;

}

}

p = o + t_min * d;

return true;

}

참고자료:
Real - Time Rendering 2판
Real - Time Collision Detection

Quaternions 정리1

복수수의 확장판

표현

q = ( v, w) = (x, y, z, w) = xi + yj + zk + w 

v: 사원수의 허수부, (  i, j, k는 허수 단위)

w: 사원수의 실수부

혹은

q = v + s 

v: 사원수 허수부

s: 사원수 실수부

허수부들의  곱 성질

i² + j² + k² = -1

i j = -j i = k

j k = -k j = i

k i = -i k = j

허수부에 더하기, 크기, 내적, 외적 등 모든 벡터 연산 사용 가능

두개의 사원수 q, r곱 ( 허수 단위들간의 곱셈을 비가환적)

qr = (iq_x + jq_y + kq_z + q_w) (ir_x + jr_y + kr_z + r_w)

     = i (q_yr_z - q_zr_y + r_wq_x + q_wr_x) + j (q_zr_x - q_xr_z + r_wq_y + q_wr_y) + k (q_xr_y - q_yr_x + r_wq_z + q_wr_z)

         + q_wr_w - q_xr_x - q_yr_y - q_zr_z

     =( q_v x r_v + r_wq_v + q_wr_v, q_wr_w - q_v • r_v)

|  i   j   k |

| q_x q_y q_z |

| r_x r_y r_z    |

외적 공식은 i (q_yr_z - q_zr_y) - j (q_xr_z - q_zr_x ) + k (q_xr_y - q_yr_x) 

덧셈:  q + r = (q_v, q_w) + (r_v, r_w) = (q_v +  r_v, q_w  + r_w)

공액(켤레, conjugate): q* = (q_v, q_w)* = (-q_v, q_w)

놈(norm): ||q||² = n(q) = qq* = q_v .q_v + q_w² = q_x² + q_y² + q_z² + q_w² (실수부만 남음)

항등 사원수: i = (0, 1)

곱셈역(multiplicative inverse): q^-1

q^-1q = qq^-1 = 1이 만족 해야 함, 역도 마찬가지로 만족해야 함

놈의 정의로 부터 유도함

||q||² = qq*   ⇔  1 = qq* / ||q||² , q^-1 = q* / ||q||²

스칼라 곱은 가환적

(가환적: 연산의 순서를 바꾸어도 그 결과가 변하지 않는 일

 실수 전체의 집합에서는 덧셈과 곱셈이 가환적)

sq = (0, s) (q_v, q_w) = (sq_v, sq_w)

qs = (q_v, q_w) (0, s) = (sq_v, sq_w)

공액 규칙:

(q*)* = q

(q + r)* = q* + r*

(qr)* = r* q*

놈의 규칙:

n(q*) = n(q)

n(q r) = n(q) n(r)

곱셈의 법칙

선형성:

p ( sq + tr ) = spq + tpr

( sp + tq ) = spr + tqr

결합법칙:

p(qr) = (pq)r

단위 사원수: q = (q_v, q_w)는 n(q)=1

그러므로  q = (sinøu_q, cosø) = sinøu + cosø 이 

||u_q|| = 1인 3차원 벡터 u_q에 대해 만족됨

이유: u_q • u_q = 1 =||u_q||² 이 만족되는 경우에 다음과 같이 되기 때문

n(q) = n(sinøu_q, cosø) = sin² ø (u_q • u_q) + cos²ø = sin²ø + cos²ø = 1

단위 사원수는 매우 효율적인 방법으로 회전 & 방향 전환 가능

복소수의 2차원 단위 벡터는 cosø + i sin ø = e ^iø

사원수에서 이와 동등한 식은 q = sinøu_q + cosø = e^øuq

단위 사원수에 대한 

로그: log(q) = log(e^øuq) = øu_q

멱함수: q^t = (sinøu_q + cosø)^t  = e^{ø t uq} = sin(øt)u_q + cos(øt)

참고 자료: Real-Time Rendering 2판

Skin Inforamtion Export Script in 3ds Max

Export skin information of node which has skin modifier

Written by Park Yun Gyu

mynode = select $

myskin = mynode.modifiers[#Skin]

OutFile = createfile "c:\\ExportSkin.txt"

NumVert = skinOps.getNumberVertices myskin

for i=1 to NumVert do

(

NumWeight = skinOps.GetVertexWeightCount myskin i

format "i:% NumWeight:%\n" i NumWeight to: OutFile

for w=1 to NumWeight do

(

BoneID = skinOps.GetVertexWeightBoneID myskin i w

BoneName = skinOps.GetBoneName myskin BoneID 1

format "--BoneID:% BoneName:%\n" BoneID BoneName to: OutFile

)

)

close OutFile

구와 구 교차 ( Intersecting sphere and sphere )

bool Sphere_Sphere( Sphere& A, Sphere& B)
{
//두개의 구 중심사이의 거리
D3DXVECTOR3 CenterDist = B.Center - A.Center;

//제곱된 거리 사용
float Dist = D3DXVec3Dot(&CenterDist, &CenterDist);

//두개의 구의 반지름의 합
float SumDist = A.Radius + B.Radius;

//제곱된 거리 사용
SumDist *= SumDist;


//합한거리보다 더 거리가 크면 서로 교차하지 않음
if( Dist > SumDist )
return false;

return true;
}

참고 문헌:

3D 게임 프로그래밍 & 컴퓨터 그래픽을 위한 수학(2판)

(Eric Lengyel저, 류광 역, 정보문화사)

REAL-TIME RENDERING 2판

(Tomas;Eric 공저, 신병석;오경수 공역, 정보문화사)

REAL-TIME COLLISION DETECTION

(Christer Ericson저, Morgan Kaufmann Publishers)

AABB와 AABB 교차 ( Intersecting AABB and AABB )

AABB( Axis Aligned Bounding Box)는 축에 정렬된 상태이기 때문에

박스가 회전하지 않고 축 방향으로 이동만 하여 위치를 잡게 된다.

그러므로 AABB의 두가지 요소 Min, Max값을 이용하여 각각의 축에 대하여 1차원적인 비교만 하면 된다.

bool AABBToAABB(AABB* pAABB1, AABB* pAABB2)

{

//x축에 대하여

if( pAABB1->Max.x < pAABB2->Min.x ||

pAABB1->Min.x < pAABB2->Max.x )

return false;

//y축에 대하여

if( pAABB1->Max.y < pAABB2->Min.y ||

pAABB1->Min.y < pAABB2->Max.y )

return false;

//z축에 대하여

if( pAABB1->Max.z < pAABB2->Min.z ||

pAABB1->Min.z < pAABB2->Max.z )

return false;

return true;

}

참고 문헌:
3D 게임 프로그래밍 & 컴퓨터 그래픽을 위한 수학(2판)
(Eric Lengyel저, 류광 역, 정보문화사)

REAL-TIME RENDERING 2판
(Tomas;Eric 공저, 신병석;오경수 공역, 정보문화사)

REAL-TIME COLLISION DETECTION
(Christer Ericson저, Morgan Kaufmann Publishers)

Physique Inforamtion Export Script in 3ds Max

Export physique information in viewport to a file

Written by Park Yun Gyu

SelNode = selection[1]

SelMesh = snapshotAsMesh SelNode

CurPhysique = physiqueOps.getPhysiqueModifier SelNode

OutFile = createFile "c:\\Export_Physique.txt"

for i=1 to SelMesh.numVerts do

(

PyType = physiqueOps.getVertexType SelNode i

BoneCount = physiqueOps.getVertexBoneCount SelNode i

format "i:% Type:% BoneCnt:% \n" i PyType BoneCount to: OutFile

for BoneCnt=1 to BoneCount do

(

BoneNode = physiqueOps.getVertexBone SelNode i BoneCnt

Weight = physiqueOps.getVertexWeight SelNode i BoneCnt

format " NodeName:% Weight%\n" BoneNode.name Weight to: OutFile

)

)

close OutFile