P: 회전이 필요한 점
q: 회전축 및 각도가 표현된 사원수

s: scalar value
v: vector value
그럼 위 식을 차례대로 풀어서 정리해 보자.
먼저 아래 공식을 기억해 두고 하나씩 정리한다.
스칼라 및 벡터 연산에 대하여 주의하면서 풀어나가면 된다.
위 식에서 앞 부분을 조금 풀어보면
그리고 게속해서 나머지를 정리한다.
여기서 v를 단위벡터A와 길이 t로 표현하여 위의 식을 계속 정리하면
SA:skew matrix of A
I: identity matrix
그리고 Axis-Angle Rotation으로 표현했던 아래 식을 상기 시켜
위의 식과 비교해 보면 다음과 같은 결과가 나온다.
위의 3개 식을 풀어서 s, t값을 구한다.
풀이에는 삼각함수의 반각공식(half-angle relations)을 사용하면 된다.
구해진 s, t를 사용하여 사원수 q를 다시 표현하면 다음과 같아진다.
: unit vector of A
이것으로 쿼터니언에서 표현되는 회전각은 1/2값임을 알 수가 있다.
위에서 구해진 식에서 앞쪽 행렬 부분이 사원수의 회전 표현식이 되고
이것을 계속 행렬로 정리한다.
여기서 정리 하기 전에 아래의 관계를 적용한다.
계속해서 행렬을 정리해 나가면
식을 좀 더 간단히 만들기 위해 단위 사원수로 바꾸어 생각한다.
여기서 사원수 q가 단위 사원수가 되면 다음이 성립한다.
이것을 이용해서 행렬식을 다시 정리하면
마지막으로 행렬식을 하나로 합치면
이 행렬식을 사용하여 사원수q를 행렬로 변환하여 사용하면 된다.
참고자료
Essential Mathematics For Games And Interactive Applications
3D 게임 프로그래밍 & 컴퓨터 그래픽을 위한 수학 제2판
Real-Time Rendering 2판









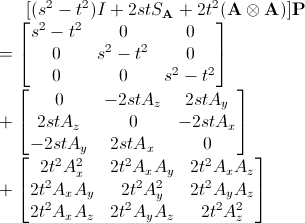





댓글 없음:
댓글 쓰기