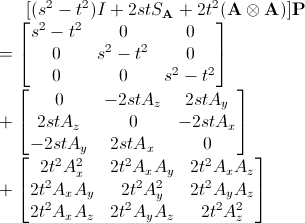2차원 직선과 직선 교차 (Intersecting line and line)

직선을 다음과 같이 표현 한다.

두개의 직선이 만나므로 아래 식으로 시작하여 풀이 된다.

같은 벡터에 대해서 내적을 하면 0이 되는 관계를 이용한다.

먼저 s에 대해서 정리하고

다음 t에 대해서 정리한다.

d₁^⊥: d₁의 수직 성분
d₂^⊥: d₂의 수직 성분

그리고 s, t에 대해 정리된 식을 모아보면 다음과 같다.

아래의 경우 두 직선은 평행한 상태가 된다.

그리고 아래 3가지 경우에 따라서 s, t값의 범위를 확인하여
교차 검사를 진행하면 된다.

1. 직선의 경우(시작과 끝이 무한대)
    s, t는 무한대

2. 선분의 경우
    d가 단위 벡터의 경우
    0 <= s <= l₁, 0 <= t <= l₂
     (l_1,l₂:각 선분의 길이)

    d가 단위 벡터가 아닐 경우 (P_end - P_start)
    0 <= s <= 1, 0 <= t <= 1
    (P_start, P_end:선분의 시작점과 끝점)

3. 광선의 경우
    0 <= s, 0 <= t

두 번째 방법으로는 선분의 s, t범위를 이용하여 구하는 방법이 된다.

첫번째 교차 방법에서 사용했던 식을 가져와서 사용한다.

먼저 2개의 직선 r₁, r₂에 대해서 다음과 같이 나타낸다.

그리고 d를 단위 벡터가 아닌 직선의 끝점과 시작점의 차이로 나타낸다.

이렇게 해서 s, t에 대한 식을 다시 정리하면

식을 간략히 하기 위해 아래과 같이 정의하고 다시 식을 정리하면

s식의 분모를 t식의 분모와 동일하게 만들기 위해 아래 정의를 이용한다.

최종적으로 아래 식과 같이 정리 된다.

이제 교차 여부를 검사 하면 한다.

f의 값이 0이 되면 두 직선은 평행 상태가 된다.

평행이 아닐 경우에는 s, t값의 범위를 검사한다.

이 방법에서는 방향 벡터 d를 직선의 끝점과 시작점의 차를 이용하므로
선분의 경우 s, t는 아래를 만족 해야 한다.
0 <= s <= 1, 0 <= t <= 1

그러므로 아래 조건을 통과 하면 교차 상태가 된다.

s의 경우
if f > 0 then
   if d < 0 or d > f then no_intersect
else
   if d > 0 or d < f then no_intersect

t의 경우
if f > 0 then
   if e < 0 or e > f then no_intersect
else
   if e > 0 or e < f then no_intersect

참고자료
Real-Time Rendering 2판

직교 투영 (Orthographic Projection)

이 투영 방법은 z값에 상관없이 변환 후에도 x, y값이 그대로 보존 된다.

원근 투영과 달리 투영 평면에 수직한 평행선을 따라
양의 z값, 음의 z값 모두 같은 평면으로 투영하게 된다.

그래서 특정 구간으로 z값을 제한 하여 사용한다.

투영은 뷰 변환 후에 (l, r, b, t, n, f)의 AABB 공간을 변환하게 된다.
l: 왼쪽 좌표
r: 오른쪽 좌표
b: 아래쪽 좌표
t: 위쪽 좌표
n: 가까운 평면
f: 먼 평면

위 4개 항목(l, r, b, t)는 현재 화면 크기에 맞추어 사용하게 된다.

예를 들어 1024x768의 화면을 가진 프로그램의 경우
(0, 1024, 0, 768)이 된다.

혹은 특별한 상황에 따라 값을 다르게 사용할 수 있다.

투영 변환 후에 생성 되는 공간을 정규화된 장치 좌표.
NDC(Normalized Device Coordinates)라고 한다.

NDC는
최소값으로 (-1, -1, -1), 최대값으로 (1, 1, 1)을 가진
축에 정렬된 정육면체 공간이 된다.

위의 경우는 OpenGL의 경우이며,

DirectX의 경우는
최소값으로 (-1, -1, 0), 최대값으로 (1, 1, 1)을 가지는
정육면체 공간을 사용한다.

즉, 직교 투영은 (l, r, b, t, n, f)의 AABB를
(-1, -1, -1), (1, 1, 1)의 AABB로 변환하는 결과가 된다.

먼저 y값의 변환을 생각해 보자.

z값은 y값에 영향을 주지 않으니 y의 변환만 신경쓰면 된다.

첫번째로 y값을 뷰 윈도우(l, r, b, t) 기준으로 되도록
값을 조정(이동) 한다.
아래 점이 원점이 되도록 y값을 수정 하면 다음 같이 된다.

 

두번째로 y값을 NDC영역인 [-1, 1]의 범위가 되도록 조정(스케일) 한다.

[b, t]에서 [-1, 1]으로 변환이 되므로
(t-b)의 크기에서 2의 크기로 스케일 된다.
그래서 다음 크기 만큼 곱해준다.

 

x값도 위와 같은 방법으로 [l, r]범위에서 [-1, 1]범위로 변환하게 된다.

z값의 경우는 추가 작업이 필요하다.

상식적으로 z값은 가까운 평면(n) < 먼 평면(f) 으로 생각 된다.

하지만 OpenGL의 경우 z축은 화면에서 밖으로 튀어나오는 방향이다.

그러므로 실제 계산에서는 z값에 음수를 곱하여 사용해야 한다.

지금까지의 결과로 직교 투영 변환은 이동 변환, 크기 변환이 차례대로
이루어지는 것을 확인할 수 있다.

행렬을 사용하여 차례대로 정리하면

DirectX의 경우 NDC의 z값은 [0, 1]범위가 된다.
[n, f]에서 [0, 1]으로 변환이 되므로 (f-n)의 크기에서 1의 크기로 스케일 한다.
n의 값이 ndc로 변환했을때 원점이 되므로 이동 변환할때는
현재 z값에서 n값 만큼만 빼주면 된다.

그리고 z축은 화면 밖에서 안쪽으로 들어가는 방향이 되므로 z값에 음수를 곱하지 않아도 된다.

그 결과 위의 행렬은 조금 수정되어 아래와 같이 된다.

참고자료
Essential Mathematics For Games And Interactive Applications
Real-Time Rendering 2판

박스(AABB, OBB)의 반지름 구하기 (Radius of AABB and OBB)

벡터 n에 투영한 박스(AABB, OBB)의 반지름 구하기

먼저 박스의 각 축을 다음과 표시한다.


각 축의 길이는 다음과 같이 표시한다.

그래서 박스의 포함된 점R은 다음식으로 나타낼 수 있다.






c: center of a box

따라서 박스의 외곽을 구성하는 8개의 점은 아래와 같이 된다.

박스의 반지름을 구하기 위해서는 반지름을 만들어낼 벡터n을 선택한 후
벡터n에 투영하여 구하면 된다.

이렇게 박스의 8개 점을 모두 투영하고 하나를 선택하여 사용한다.
투영된 길이 중에서 최대 값을 사용하여야 박스의 모든 점을 포함하는
최대 반지름값을 얻을 수 있게 된다.

그럼 위 식에서 최대 반지름을 만족 시키기 위해서
먼저 각 축의 길이는 모두 양의 값을 가지게 된다.
그래서 위 식을 아래와 같이 정리할 수 있다.

만약 벡터n이 단위 벡터가 아닌 경우 n의 크기로 나누어 주면 된다.

참고자료
Essential Mathematics For Games And Interactive Applications
3D 게임 프로그래밍 & 컴퓨터 그래픽을 위한 수학 제2판
Real-Time Rendering 2판

사원수 회전 (Quaternions Rotation)

사원수(Quaternions)의 회전은 아래와 같이 나타낼 수 있다.
P: 회전이 필요한 점
q: 회전축 및 각도가 표현된 사원수




s: scalar value
v: vector value

그럼 위 식을 차례대로 풀어서 정리해 보자.

먼저 아래 공식을 기억해 두고 하나씩 정리한다.

스칼라 및 벡터 연산에 대하여 주의하면서 풀어나가면 된다.
위 식에서 앞 부분을 조금 풀어보면

그리고 게속해서 나머지를 정리한다.

여기서 v를 단위벡터A와 길이 t로 표현하여 위의 식을 계속 정리하면

S_A:skew matrix of A
I: identity matrix

그리고 Axis-Angle Rotation으로 표현했던 아래 식을 상기 시켜
위의 식과 비교해 보면 다음과 같은 결과가 나온다.

위의 3개 식을 풀어서 s, t값을 구한다.
풀이에는 삼각함수의 반각공식(half-angle relations)을 사용하면 된다.

구해진 s, t를 사용하여 사원수 q를 다시 표현하면 다음과 같아진다.

: unit vector of A


이것으로 쿼터니언에서 표현되는 회전각은 1/2값임을 알 수가 있다.

위에서 구해진 식에서 앞쪽 행렬 부분이 사원수의 회전 표현식이 되고
이것을 계속 행렬로 정리한다.

여기서 정리 하기 전에 아래의 관계를 적용한다.

계속해서 행렬을  정리해 나가면

식을 좀 더 간단히 만들기 위해 단위 사원수로 바꾸어 생각한다.
여기서 사원수 q가 단위 사원수가 되면 다음이 성립한다.

이것을 이용해서 행렬식을 다시 정리하면

마지막으로 행렬식을 하나로 합치면

이 행렬식을 사용하여 사원수q를 행렬로 변환하여 사용하면 된다.

참고자료
Essential Mathematics For Games And Interactive Applications
3D 게임 프로그래밍 & 컴퓨터 그래픽을 위한 수학 제2판
Real-Time Rendering 2판

임의의 축 회전 (Axis Angle Rotation)

R² 공간에서 벡터 i=(1, 0)를 회전시 다음과 같이 나타낼 수 있다.

여기서는 기저 벡터를 i, j 대신에 v_perp, w를 사용하고 회전축 A를 이용한다.

v_prop: A축에 대해 projection
v_perp: A축에 대해 perpendicular

위 식은 v의 수직 성분만 있으므로 수평 성분을 더하면 회전된 v를 계산할 수 있다.

그런데 v_prop는 회전축A에 대하여 회전을 하여도 변하지 않게 된다.

그래서 회전된 v는 다음과 같다.

먼저 v_prop를 찾아보자.

회전축인 A에 v를 투영하면 확인할 수 있다.

: A의 unit vector


그리고 v에서 수평 성분인 v_prop를 빼면 수직 성분인 v_perp를 구할 수 있게 된다.

w는 회전축A와 v의 외적으로 구해진다.

위의 회전식을 지금까지 구해진 식으로 풀어서 적으면

그리고 v를 분리하기 위해 tensor product와 skew matrix를 사용하여 정리 한다.

[tensor product]
두개의 벡터 v, w가 있을때

그리고 3개의 벡터 u, v, w가 있을 때

[skew matrix]
외적을 행렬로 표현할때 사용
벡터 v를 skew matrix로 표현하면

그리고 여기에 벡터 w를 곱해주면 외적이 행렬로 표현 된다.

식을 다시 정리하면

S: skew matrix

I: identity matrix

이제 위의 식에서 벡터 v에 곱해지는 부분이 바로 벡터 v를 회전 시키는 행렬 부분이 된다.
다시  행렬 부분만  풀어 적게 되면  다음과 같이 된다.

위의 행렬을 임의의 벡터 v에 곱하게 되면 임의의 회전축 A를 기준으로
회전된 벡터 v를 구할 수 있다.

참고자료
Essential Mathematics For Games And Interactive Applications
3D 게임 프로그래밍 & 컴퓨터 그래픽을 위한 수학 제2판